One of the intriguing aspects of reality, as far as we are able to analyze and perceive it to date, is that it depends upon a relatively small set of dimensionless parameters. Here is a listed set, taken from the paper “Dimensionless constants, cosmology, and other dark matters” by Max Tegmark (MIT), Anthony Aguirre (UCSC), Martin J Rees (Cambridge), and Frank Wilczek (MIT) (Phys.Rev. D73 (2006) 023505):

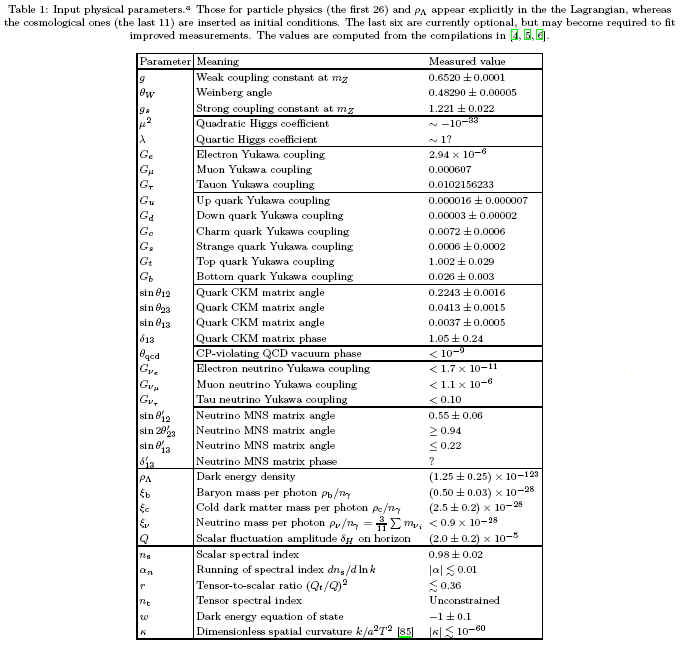
And here are the derived physical parameters:

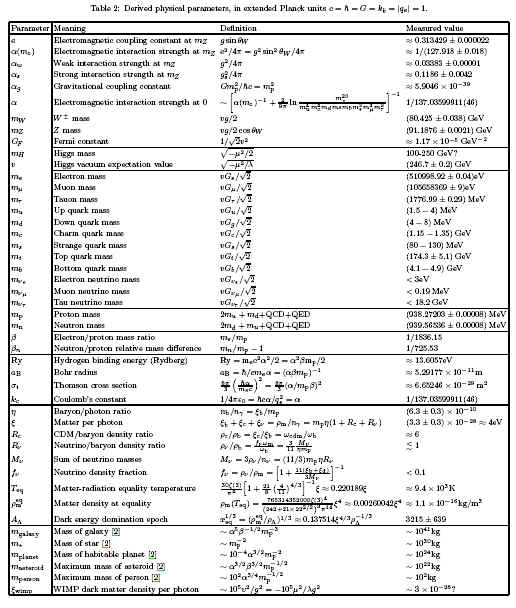
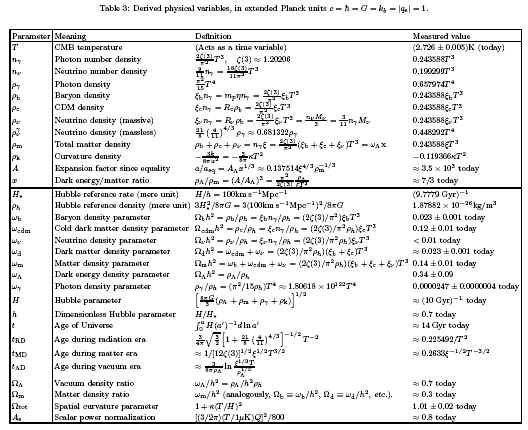
I got to this paper via an article in New Scientist (subscription required for full article) by one of the paper’s authors (Max Tegmark) who feels that our universe itself is a mathematical construct:

Here, I will push this idea to its extreme and argue that our universe is not just described by mathematics – it is mathematics. While this hypothesis might sound rather far-fetched, it makes startling predictions about the structure of the universe that could be testable by observations. It should also be useful in narrowing down what an ultimate theory of everything could look like….

So here is the crux of my argument. If you believe in an external reality independent of humans, then you must also believe in what I call the mathematical universe hypothesis: that our physical reality is a mathematical structure. In other words, we all live in a gigantic mathematical object – one that is more elaborate than a dodecahedron, and probably also more complex than objects with intimidating names like Calabi-Yau manifolds, tensor bundles and Hilbert spaces, which appear in today’s most advanced theories. Everything in our world is purely mathematical – including you.

Tegmark also feels that this hypothesis leads inevitably to the conclusion that multiverses exist that embody different combinations of dimensionless parameters; we just happen to be in one in which life as we know it can evolve. I’m impressed that Tegmark et al. in the “Dimensionless parameters” paper were willing to include “design” as one explanation for the “fine-tuned for life” values of the parameters, though (rightly) stating that physicists prefer the others:

So why do we observer these 31 parameters to have the particular values listed in Table 1? Interest in that question has grown the the gradual realization that some of these parameters appear fine-tuned for life, in the sense that small relative changes to their values would result in dramatic qualitative changes that could preclude intelligent life, and hence the very possibility of reflective observation. As discussed extensively elsewhere [list of footnotes], there are four common responses to this realization:

1. Fluke: Any apparent fine-tuning is a fluke and is best ignored.
2. Multiverse: These parameters vary across an ensemble of physically realized and (for all practical purposes) parallel universes, and we find ourselves in one where life is possible.
3. Design: Our universe is somehow created or simulated with parameters chose to allow life.
4. Fecundity: There is no fine-tuning, because intelligent life of some form will emerge under extremely varied circumstances.

Options 1, 2 and 4 tend to be preferred by physicists, with recent developments in inflation and high-energy theory given new popularity to option 2. (Tegmark et al., Phys.Rev. D73 (2006) 023505, pp. 1-4)

No great theological or philosophic intent to this posting, other than I tend to lean towards the “Design” answer. My intended college major during my senior year of high school was astrophysics; that came to a halt upon reading an article about the bartenders and cab drivers with PhDs in astrophysics, but I remain interested in the topic. On the other hand, as someone who has done real-world simulation work (cruise missiles, large space structures, the Space Shuttle flight simulators, and tectonic processes on Venus), I’m keenly aware of how model definition and parameter selection directly leads to your results. ..bruce..